スマホオンライン家庭教師ライフです!
こんちわ!
今回は勉強のお話
高校数学 相加相乗平均の説明
高校数学の数Ⅱですね
相加相乗平均の解説をしていきます
そもそも、相加相乗平均って何か知ってます?
相加相乗平均を取り扱った問題数は少ないのでスラッと終わってしまうところですが、
ここ、入試でいきなり出てきたりします
よくやる問題は勝手に覚えるのでいいんですけど、
こういう「あんまやってないけど入試で出る」ってところが結構重要です
相加平均と相乗平均とは?
まず、平均って2種類あるんですよね
中1で習う平均が相加平均です
要素を足して、その要素の個数で割るっていうやつです
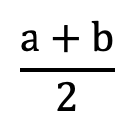
こんな感じ
3つのものを足したら3で割ります
で、相乗平均が聞き慣れないと思うんですが、
これは掛け算の平均です
要素をかけて、その要素の個数を累乗で割るっていう平均です
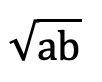
こんな感じ
3つのものを掛けたら3乗根がつきます
例えば58と64っていう2つの数でやると、
相加平均だったら58+64を2で割って、61ですね
相乗平均だったら58×64にルートをつけて、ルートの3712ですね
だいたい60ぐらい
平均って2種類あって、こんな感じで求め方が変わってくるんですね
相加平均≧相乗平均
で、ここから大事なんですが、
2つの数の相加平均と相乗平均って大小関係が決まってるんです
2つの数がどんな値でも、必ず相加平均が相乗平均以上になるんです
てことで、こういう公式ができます
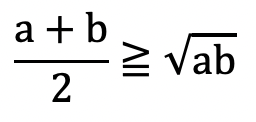
分数がキモいので、両辺を2倍しましょう

ちょっとすっきりしました
はい、2つの数a,bがあったら、この公式が使えるようになるんですね
相加相乗平均を使った問題の解説
では、この問題を解いていきましょう
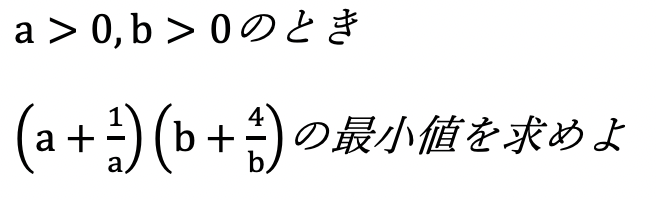
相加相乗平均は最小値を求める時に使える
なんで最小値を求める問題なのに平均を求めんの?
って思うかもしれません
でも実は、相加相乗平均って最小値を求める時によく使います
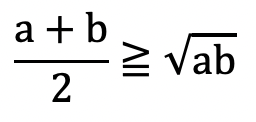
この公式、見方を変えると
相加平均は最低でも相乗平均、つまり、相加平均の最小値は相乗平均
って言えません?
最小値を求める時って、今までは関数でやってましたよね
2次関数で平方完成して最小値を求めていました
そしてここから、相加相乗平均でも最小値が求められるようになります
相加相乗平均を使うポイントは逆数
でもぱっとみ相加相乗平均をどう使うか分からないですよね
まずは問題の式を展開してみましょう
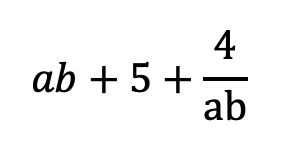
こうなりました
ここで、abが逆数で2つ出てきましたね
これで相加相乗平均が使えるパターンだと分かります
はい、相加相乗平均のポイントは逆数なんです
なんでかっていうと、

公式の右辺にルートabがあるじゃないですか
ここでaとbが逆数の関係になってると、約分できて綺麗になるんですよね
先に説明されてもよく分からんと思うので、あんま気にしなくていいです
問題を解けば分かります
とにかく、相加相乗平均のポイントは逆数!
計算してみる
相加相乗平均の公式のaをab,bを4/abに置いて、実際に当てはめてみましょう
問題文の式には+5がありますが、後で足せばいいので置いておきます

で、ここでルートの中のabが綺麗に訳分できますね
だから逆数がポイントなんです

こうなります
ほいでルートの計算をして

問題文の式の5が足りないので、両辺に足して元の式を作ります

左辺を因数分解して元に戻して、右辺を計算しましょう

はい、最小値は9!
こんな感じで使っていきます
最初にも言いましたけど、
相加相乗平均の問題はあんまり出ません
出ないからこそ入試ですっぽかす可能性がでかいので
よく覚えておく必要があります
まとめ
まとめましょう
・相加平均は足して割った平均
・相乗平均は掛けてルートをつけた平均
・相加平均≧相乗平均になるので、最小値が求められる
・相加相乗平均のポイントは逆数(ルートの中が約分できるので)
質問あったらコメント等ください!




コメント